Welcome to our virtual Martian observatory.

1. Do you want to know what your weight on Mars is? You can see our calculation here:

We should use Newton's law of gravity:

F = G.(M₁.M₂)/r²

r - Earth's radius

or

(а_Mars) / (а_Earth) = ( М_Mars . r²_Earth) / (М_Earth . r²_Mars ) = 0.379

We know that F_{weight(Earth)} = m.g

And from here we find that the weight of a body on Mars is:

F_weight(Mars) = 0.379.F_{weight(Earth)}

Calculate your weight on Mars! Enter your weight on Earth and click "Calculate"!

2. Now let's take a look at the Martian sky. You may wonder what does it look like?

The Martian night sky is practically the same as the one seen from Earth. The difference is that we see Jupiter and Saturn a little bit brighter, because they are much closer to Mars than to Earth. The brightness of Venus and Mercury is several times lower. We can also see the bright Earth and the Moon. The Martian satellites, Phobos and Deimos, cross the sky very quickly. Phobos rises in the west and sets in the east. It crosses the whole sky twice a night. The axis of Mars points towards Alpha Cyg (Deneb).

The Martian day is somehow different from the Earth's one. The diameter of the Sun's disk is twice smaller. Because of the atmosphere with low density, the sky is dark enough both during the day and the night, coloured in rusty. We can see the Sun, bright starts, planets and Mars' moons at the same time.



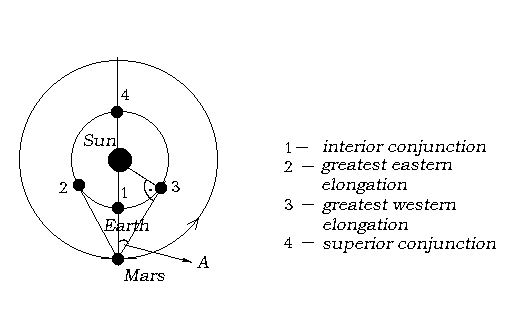
3. How do we see the Earth on the Martian sky?

In reference to Mars the Earth is an interior planet, so it is periodically in superior and inferior conjunctions with the Sun and in great elongations (western and eastern).

These configurations take turns in a period of 780 days (synodic period).

We can easily find the average value of the greatest Earth's elongation (A) as seen from Mars (fig.1).

If a_Earth and a_Mars are the semi major axises of Earth's and Mars' orbits, then:

А = arcsin ( a_Earth / a_Mars ) = arcsin ( 1 au / 1.524 au ) = 41^o

Having in mind the eccentricity of the Martian orbit, е_Mars = 0.0935, the perihelion distance of the planet is:

q_Mars = a_Mars ( 1 - е_Mars ) = 1.382 au

And in this case the greatest elongation of the Earth is 46^o:

4. And how bright exactly is the Earth that we see?

We can compare it to Venus, which is also an interior planet, when observed from the Earth.

The sizes of the two planets are almost the same. But the albedo of the Earth is twice less the albedo of Venus, because it is entirely covered with clouds, while the Earth is usually half-covered.

The apparent brightness observed is related to distance with an inverse square relationship, that's why in equal positions the ratio of the floods of light from Venus to the Earth and from the Earth to Mars is:

E_Venus/E_Earth = 2.(r_Earth / r_Venus)².(r_Mars- r_Earth)² / (r_Earth - r_Venus)² = 12.3

where:

r_Earth - r_Venus is the distance between the Earth and Venus

In stellar magnitudes, considering Pogson's formula, this is:

2.5lg(E_Venus/E_Earth) = 2.7^m

And because in great elongation Venus, as seen from the Earth, has a magnitude of - 4.1^m , the Earth for the Martians (in the same configuration) will shine as a star with -1.4^m, just like Sirius or Mars observed from the Earth in opposition.

5. Transits of Phobos, Deimos and Earth

No one has ever seen a transit of Earth from Mars, but the next one will take place on November 10, 2084, and could be observed by future Mars tourists. The last such transit took place on May 11, 1984.

A transit of Earth across the Sun as seen from Mars takes place when the planet Earth passes directly between the Sun and Mars, obscuring a small part of the Sun's disc for an observer on Mars. During a transit, Earth can be seen from Mars as a small black disc moving across the face of the Sun.

Transits of Earth from Mars follow a 284-year cycle, occurring at intervals of 100.5, 79, 25.5, 79 years in either May or November. It is analogous to the cycle of transits of Venus from Earth, which follows a cycle of 243 years (121.5, 8, 105.5, 8).

Awaited oppositions of Earth:

November 8, 1800
November 12, 1879
May 8, 1905
May 11, 1984
November 10, 2084 (the picture on the right)
November 15, 2163
May 10, 2189
May 13, 2268
November 13, 2368






A transit of Phobos across the Sun as seen from Mars take place when Phobos passes directly between the Sun and a point on the surface of Mars, obscuring a large part of the Sun's disc for an observer on Mars. During a transit, Phobos can be seen from Mars as a large black disc rapidly moving across the face of the Sun. Due to the Phobos' size the event could also be referred to as a partial eclipse of the Sun by Phobos.

During the transit of Deimos, since its angular diameter is only 1/10 of the Sun's one as seen from Mars, a smaller part of the Sun's disc is obscured (compare to Phobos). The event looks like as the Venus transit seen from Earth. The angular diameter of Deimos is only 2 ? times the angular diameter of Venus from Earth. A transit of Phobos from Mars usually lasts only thirty seconds or so, due to its very rapid orbital period of about 7.6 hours. In difference of it the transit of Deimos lasts a little bit longer - a minute or two, due to its relatively longer orbital period - about 30.3 hours.

Because both bodies orbit Mars in low-inclination equatorial orbits, the shadows of Phobos or Deimos projected onto the surface of Mars exhibit a seasonal variation in latitude. At any given geographical location on the surface of Mars, there are two intervals in a Martian year when the shadows of Phobos or Deimos are passing through its latitude. The shadow always falls on the "winter hemisphere", except when it crosses the equator during the vernal equinox and the autumnal equinox. Thus transits of Phobos and Deimos happen during Martian autumn and winter in the northern hemisphere and the southern hemisphere, roughly symmetrically around the winter solstice. Close to the equator they happen around the autumnal equinox and the vernal equinox; farther from the equator they happen closer to the winter solstice. Over the surface of Mars as a whole, there are transits of Phobos somewhere on Mars on most of the days of the Martian year. However, at some intervals in the Martian year the shadow of Phobos is passing north or south of Mars.

Because it orbits so close to Mars, Phobos cannot be seen north of 70.4°N ( 82.7° N for Deimos) or south of 70.4°S (82.7°S - for Deimos); such latitudes will obviously not see transits either.



On the pics you can see transits of Phobos and Deimos as captured by …..

Deimos - Mars Rover Opportunity on March 4, 2004

Phobos - Mars Rover Opportunity on March 10, 2004